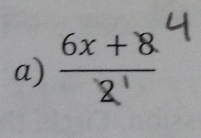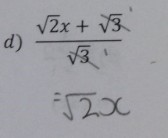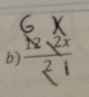“Crack-the-Code Contest” – Reshaping Culture with Contests
Background

Since the very beginnings of my career, education has always been more than refined lessons and enhanced learning, it has been about attitudes. When you teach a subject like mathematics you realize quickly that you have the cards stacked against. Students walk into your classroom with a negative attitude towards the subject that you have grown to love. We stand there bewildered that someone could “hate” math. Students and grown adults freely admit to me, no reservations, there disdain towards the subject. “No offense”, they would say, “I like you, I just hate math”. It is true? Could this many people actually hate math? I started to believe that.
That is until I started to look at where math surfaced outside the classroom. I would see movies like, Good Will Hunting, 21, and Pi, television shows like Numbers, and books like Permat’s Enigma, that would remind me of how intriguing the mathematical mind could be. On a daily basis we see countless examples of people voluntarily gaming, puzzling, programming, reasoning, conjecturing, and proving and made me think, maybe it’s not mathematics that people have a problem with but school mathematics. In her book, Elephant in the Classroom Jo Boaler explains, School maths is widely hated, but the mathematics of life, work and leisure is intriguing and much more enjoyable. There are two versions of maths in the lives of many people: the strange and boring subject that they encountered in classrooms and an interesting set of ideas that is the maths of the world, and is curiously different and surprisingly engaging”. However, we seldom slap the label of “mathematics” on anything outside the classroom. Go ahead, ask someone you know, child or adult, to name something “mathy” and see what they say. If they are anything like my sampling they might suggest, “adding and subtracting”, “fractions”, “algebra”, or “geometry”, all of which are explicit aspects of the k-12 curriculum.
The Inspiration
My goal in math education has always been to reshape the culture and connotations attached to mathematics. I have worked hard to see that happen in my classroom but I realized if we want students to change their attitude towards mathematics, we might need to help them change their definition of what mathematics is. We need to help students label things like games, programming, and puzzles as being mathematical. I wanted to create a trend around mathematical activities. Then, 3 years ago, a new game began creeping into North American news.
Escape rooms were popping up everywhere and no matter how many of them there were, they were always booked up. If you haven’t had the opportunity to try one, the premise is simple. You are locked in a room and using the clues and puzzles around you, you must figure out a way to escape in less than an hour. If you think I am exaggerating about the popularity of these places, you need only to Google map search “escape room” in your area. I managed to find 13 of them within 30 minutes of the downtown Vancouver area. Not only are these businesses on the rise, they have began to diversify their rooms to include various themes which are often supported by additional actors. The Smartypantz company in Gas Town, Vancouver offered rooms like “Thirst for Murder”, where you are trapped in “a nightmarish basement and about to fall victim to a killer’s psychotic and cannibalistic quest for the fountain of youth. There is a glimmer of hope though; you’ve been left alone and there may be a way out”. Or perhaps you would prefer, “Dreamscape” where you are trapped in “a dream, surrounded by a bizarre and artistic alternate reality. If you don’t find a way to understand the clues and solve the puzzles, you will never wake up”. Other cities offer plenty of alternatives, this one my personal favourite:
As I read more and more about escape rooms I grew in excitement. However, unlike most people my excitement wasn’t to go and solve puzzles (I do plenty of that already), I wanted to be a gamemaster. I wanted to be the one that brought mathematical thinking to thousands of people. These individuals were able to promote logical and lateral thinking, problem-solving, collaboration, and communication, all of the things I considered to be the absolute essence of mathematics.
The Structure
So, I went straight to work, creating my version of the escape room. There was only one problem, of course: parents and administrators tend to frown upon locking students in a room for an hour. Not to mention with escape rooms there are only so many people who could participate at a time, I wanted to involve the entire school. My thinking switched from locking people in an enclosure to locking them out of an enclosure. This gave rise to quick garage project the beginning of the “Crack-the-Code” contest. Of course, I needed to give so additional incentive to get into the box so I loaded it with candy and gift cards.

The premise for this contest was that the students would need to figure out the combination for the locks and obtain the master key by working through a series of puzzles and problems that promoted mathematical thinking. It was imperative for me that this contest be a public spectacle. Not only did I want students to know that the contest was going on, I wanted students to know that their peers were actively involved in the contest. Too often there is a stigma attached to participating in extra-curricular math activities and students are often shamed for their participation. I wanted the students to see that it wasn’t only the academically elite that were involved. Thus, I made the instructions printed on bright orange paper and on the back was the first clue.

A key element in this contest was the QR code. QR codes can be created use a number of different websites but I used http://www.qrstuff.com/, mostly because it didn’t require me to download any additional software and I could copy and paste directly from the website. QR codes can be scanned with almost any smartphone and will pull up the website that it is linked to. These could also be used along with Google URL shortener which will keep track of number of times each QR code is accessed. Students quickly discovered that not only do you need to solve the puzzle, you also need to determine where the solution is leading you. For example, students would have come across this clue.

The solution to this clue was $162 which may have prompted a lot of different locations. Some students went to room 162, others went to parking space 162. Eventually students would find the clue at locker 162 and behind the lock hid another QR.
Students would scan this and up popped another puzzle. This time they were given a puzzle with 
This puzzle gave a solution of Esther Lim and 3:00. Completely perplexed, many students were stumped by this solution. I could hear groups of students shouting “Who is Esther Lim?” After many Google and yearbook searches students began to notice the brief quotes written at the bottom of each page like the puzzle above which gave them some direction on their next location found in the fine arts building.

As students solved each of the clues and moved on to the next location they were slowly revealed the numbers to crack the code with the final puzzle leading them to the master key which was kept by the keymaster (myself). This was done so that I would know when the last group was about to finish the contest. I also ensured that I could give another puzzle if I found that the initial puzzles were done too quickly. This way the contest length was always controlled by myself.
The Art of Puzzle-Making
For me the fun part was making the puzzles and writing problems that were simple enough for the grade nines to engage with but difficult enough to cause the grade 12’s to deliberate over (our school is grade 9-12).
Don’t reinvent the wheel
For many teachers this is the frightening part of organization the event, the component that seems to take the most amount of time. Let me reassure any potential organizers, you don’t need to reinvent the wheel. There are lots of great problems out there. Martin Gardener and Sam Loyd have written numerous books packed full of great problems (some of them found here: www.puzzles.com and www.mathsisfun.com/puzzles ).
Rename the wheel
While you might not need to reinvent the wheel, you do need to rename it. Too many puzzles have posted solutions found somewhere on the internet. If you do not change the problem it does not take much effort on behalf of the student to copy and paste the clue and find a solution in lesson than a minute. For example, there is a great problem on divisibility that asks you to “Create a 10 digit number where the first n digits are divisible by n”. I copied and pasted that exact phrasing into Google and here are search results.

On top of the countless websites that offer a solution there is a youtube channel that gives solutions as well. Creating a story that goes with the puzzle allows you to bring the problem to life and change it in such a way that it is no longer recognizable. For example, I adapted the above in the following way.
Write with the end in mind
One essential piece of the contest is that the gamemaster must be able to create a puzzle that leads students to a particular location. This, of course, begs the skills and knowledge of a math teacher. Someone who not only knows how to solve the puzzle but also knows how to change the conditions of the puzzle to create a particular solution. This could be accomplished by using a cipher to change numerical responses into alphabetical or you could simply use a bit of arithmetic to change the final solution. For example, in the problem it was said that the king gave an additional reward to the servant boy who solve the puzzle. That “award” that was given in addition was enough to change the solution to a phone number that belonged to the keymaster.
The Impact
At the BCAMT conference I was able to share a few stories on the impact the contest had on individual students. While I think there is an incredible testimony that comes in the those individual cases, I wish to share a bit of how it reshaped our community.
In particular the participation of the school body was a bit surprising to me. Initially I had put out 100 orange pieces of paper with the first clue on it. By the end of day one every one of those papers was gone. Although I am certain that some of those ended up in the trash, I was happy to see even a 10% participation rate (our school has approximately 500 students). On top of that I was able to use a URL shortener (https://goo.gl/) for the first clue which tracked the number of times students accessed the first clue. This total was near 90 students which meant that, conservatively, 20% of the students had seen the first clue (I wished I had kept the using shorteners for the remainder of the contest). In the end there were 5-6 groups who had made it to the final few stages. This included 2 grade 12 groups, 1 grade 11 group, and 2 grade 10 groups.
The Math Club
Math club has always been a bit of difficult club to get off the ground. I have always had a consistent group that participates every year but it was seldom more than 10-12 students. Not only that, the students involved were the same students that did exceptionally well in the classroom. That tells me that students still think that grades translate to mathematical thinking and while most of our students who do well on contests are also strong students, I have had plenty of students who are not straight A students do well on contests. I wanted to entice more students to join the math club, even if they only tried one contest. Instead of asking students to show up to meetings I simply asked them to join a Google classroom group created for the math club. I did this for two reasons. One, I wanted them to at least receive information and decide whether or not they wanted to participate. Two, I wanted lots of people to be a part of the math club. I wanted students to tell their friends they had joined the math club, even if they didn’t write a single contest. By doing this I could slowly remove the stigma attached to math club being for “math geeks”.
So how does math club tie in with “Crack-the-code”? Well, I also decided to use the math club Google classroom to provide extra details on the contest along with some hints. Students were told that they would receive details about future contests that they may wish to participate in. On day one of the contest I had 7 students signed up for math club. By lunch… by day 2… by the end of day 2.
Launching your own contest
If you feel a little overwhelmed you are in good company. The first contest I launched had plenty of issues that I had to work around. That together with the fact that I was attempting to run the entire contest by myself made it challenging to think about anything else the entire week. However, each year I learn a few lessons and the contest runs smoother than the previous year. Here are a few lessons I learned.
- Don’t put soda in the box – During a staff meeting I was called to the office after the secretary had informed me that my box was dripping. Apparently the student thought they could shake the contents loose.
- Don’t make your window out of glass – I had a student this past year shake the locks on the box and ended up putting the lock right through the glass. It has since been replaced with plastic.
- Get a team to help – One of the biggest difficulties I had was getting someone to look at the puzzles and determine a solution before I launched the contest. At one stage I had the most bizarre solutions from students only to discover my question had been written incorrectly. Because the clues were written on Google docs, I was able to update them instantly to avoid any other groups having difficulties.
- Control the pace – I intentionally put in some clues that had solutions that were only accessible during certain times of the day or week. One clue, in particular, was found in our auditorium, a location that students could only access once a week. This allowed students who were falling behind to catch up. Other clues were found on license plates that were driven away at the end of the school day.
- Support those lagging – As long as students were interested in participating I wanted to make sure they knew they were still in it. In some cases I did a little mini lesson on solving systems of equations for students who had written out algebraic statements. Other times I prompted them to stick to the high school building when looking for a clue. Once the majority of students were on stage 2 or 3, I also started giving hints on stage 1. This ensured they were always trailing close behind.
- Keep in grade-neutral – You want to maximize participation and while a more developed thinker in grade 12 will have an advantage over a grade 9, you want to ensure everyone is able to participate. Giving puzzles involving quadratic equations or calculus concepts may inhibit students from getting involved.
You want to get started?
My goal as a math educator has always been to change the culture and connotations surrounding mathematics in North America. I do this with my friends, my family, my colleagues, and my students. However, I have come to a point in my career where I realize I do not operate on an island. If we want to see change in Vancouver, British Columbia, or even Canada we, as educators, need to work together; to share, to support, to inspire. If this contest is something you are interested in launching at your school I would be happy to come and share my experience and for practical ways you can get started. Please don’t hesitate to email me or hit me up on Twitter for any tips or resources. If you have something similar at your school I would love to hear your story.
danielwoelders@gmail.com | Twitter: @woelders